数量关系之容斥问题解题原理及方法
一、知识点
1、集合与元素:把一类事物的全体放在一起就形成一个集合。每个集合总是由一些成员组成的,集合的这些成员,叫做这个集合的元素。
如:集合A={0,1,2,3,……,9},其中0,1,2,…9为A的元素。
2、并集:由所有属于集合A或集合B的元素所组成的集合,叫做A,B的并集,记作A∪B,记号"∪"读作"并"。A∪B读作"A并B",用图表示为图中阴影部分表示集合A,B的并集A∪B。
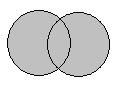
例:已知6的约数集合为A={1,2,3,6},10的约数集合为B={1,2,5,10},则A∪B={1,2,3,5,6,10}
3、交集:A、B两个集合公共的元素,也就是那些既属于A,又属于B的元素,它们组成的集合叫做A和B的交集,记作"A∩B",读作"A交B",如图阴影表示:
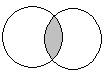
例:已知6的约数集合A={1,2,3,6},10的约数集合B={1,2,5,10},则A∩B={1,2}。
4、容斥原理(包含与排除原理):
(用|A|表示集合A中元素的个数,如A={1,2,3},则|A|=3)
原理一:给定两个集合A和B,要计算A∪B中元素的个数,可以分成两步进行:
第一步:先求出∣A∣+∣B∣(或者说把A,B的一切元素都"包含"进来,加在一起);
第二步:减去∣A∩B∣(即"排除"加了两次的元素)
总结为公式:|A∪B|=∣A∣+∣B∣-∣A∩B∣
原理二:给定三个集合A,B,C。要计算A∪B∪C中元素的个数,可以分三步进行:
第一步:先求∣A∣+∣B∣+∣C∣;
第二步:减去∣A∩B∣,∣B∩C∣,∣C∩A∣;
第三步:再加上∣A∩B∩C∣。
即有以下公式:
∣A∪B∪C∣=∣A∣+∣B∣+∣C∣-∣A∩B∣-∣B∩C∣- |C∩A|+|A∩B∩C∣
二、例题分析:
例1 求不超过20的正整数中是2的倍数或3的倍数的数共有多少个。
分析:设A={20以内2的倍数},B={20以内3的倍数},显然,要求计算2或3的倍数个数,即求∣A∪B∣。
解1:A={2,4,6,…20},共有10个元素,即|A|=10
B={3,6,9,…18},共有6个元素,即|B|=6
A∩B={既是2的倍数又是3的倍数}={6,12,18},共有3个元素,即|A∩B|=3
所以∣A∪B∣=∣A∣+∣B∣-∣A∩B∣=10+6-3=13,即A∪B中共有13个元素。
解2:本题可直观地用图示法解答
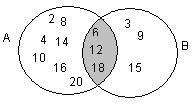
如图,其中,圆A中放的是不超过20的正整数中2的倍数的全体;圆B中放的是不超过20的正整数中3的倍数的全体,其中阴影部分的数6,12,18是既是2的倍数又是3的倍数的数(即A∩B中的数)只要数一数集合A∪B中的数的个数即可。
例2 某班统计考试成绩,数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90分以上的有38人。问两科都在90分以上的有多少人?
解:设A={数学成绩90分以上的学生}
B={语文成绩90分以上的学生}
那么,集合A∪B表示两科中至少有一科在90分以上的学生,由题意知,
∣A∣=25,∣B∣=21,∣A∪B∣=38
现要求两科均在90分以上的学生人数,即求∣A∩B∣,由容斥原理得
∣A∩B∣=∣A∣+∣B∣-∣A∪B∣=25+21-38=8
点评:解决本题首先要根据题意,设出集合A,B,并且会表示A∪B,A∩B,再利用容斥原理求解。
例3 某班同学中有39人打篮球,37人跑步,25人既打篮球又跑步,问全班参加篮球、跑步这两项体育活动的总人数是多少?
解:设A={打篮球的同学};B={跑步的同学}
则 A∩B={既打篮球又跑步的同学}
A∪B={参加打篮球或跑步的同学}
应用容斥原理∣A∪B∣=∣A∣+∣B∣-∣A∩B∣=39+37-25=51(人)
- 2025-05-07
- 2025-04-25
- 2025-04-24
- 2025-04-19
- 2025-04-30
- 2025-05-07
- 2022-07-23
- 2021-03-19
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-04-30
- 2025-04-30
- 2025-04-30
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2021-02-24
- 2021-02-24
- 2021-02-24
- 2021-02-24
- 2021-02-24
- 2021-02-24













