公务员考试行测数量关系:数字推理之数列
1、自然数列
【示例】1,2,3,4,5,6……
2、奇数数列
【示例】1,3,5,7,9……
3、偶数数列
【示例】2,4,6,8,10……
4、平方数列
【提点】熟记1-21的平方
【示例】1,4,9,16,25……
5、立方数列
【提点】熟记1-11的立方
【示例】1,8,27,64,125……
6、多次方数列
【提点】熟记2的1-10次方
【示例】2,4,8,16,32,64,128……
7、质数数列
【提点】质数:大于1的自然数,约数只有1和它本身的数。
【示例】2,3,5,7,11,13……
8、合数数列
【提点】合数:大于1的自然数,约数除了1和它本身之外还有其他约数。
【示例】4,6,8,9,10,12……
![]()
9、等差数列
【提点】数列从第二项开始,每一项与它前面一项的差都等于一个常数,这个常数称为这个等差数列的公差。
【示例】3,9,15,21,27,33,39,……是一个公差为6的等差数列。
等差数列的相邻项之差是一列常数,即数列相邻项的差是规律的,利用这一【提点】加以创新,产生了下面两种基本变化。
基本变化1:数列相邻两项之差是一个简单变化的数列。
【示例】2,3,7,16,32,57,……,相邻两项之差依次是 1、4、9、16、25、……,是平方数列。 图示如下:
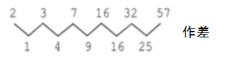
基本变化2:数列在连续变化过程中,以数列相邻项之差为基础。
【示例】2,5,15,50,175,625,……,从第三项开始,每一项都等于它前面两项之差的5倍。图示如下:
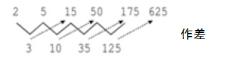
![]()
10、等比数列
【提点】数列从第二项开始,每一项与它前面一项的比值等于同一个非零常数,这个非零常数称为这个等比数列的公比。
【示例】2,6,18,54,162,486,……,是一个公比为 3 的等比教列。
等比数列的相邻项之比是一列常数,即数列相邻项的比是规律的,利用这一【提点】加以创新,产生下面两种基本变化。
基本变化1:数列相邻两项之比是一个简单变化的数列。
【示例】3,6,18,90,630,6930,……,教列相邻项之比依次是 2、3、5、7、11,是质教列。图示如下:
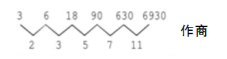
基本变化2:数列在连续变化过程中,以前一项的倍数为基础。
【示例】1,4,13,40,121,364,……,数列从第二项开始,每一项都是它前面一项在3倍的基础上再加1所得到的。1*3+1=4、4*3+1=13、13*3+1=40、40*3 +1=121、121*3+1=364。
![]()
11、和数列
【提点】数列从第三项开始,每一项都等于它前面两项之和。
【示例】1,2,3,5,8,13,……
基本变化1:数列相邻项之和是一个简单变化的数列。
【示例】2,2,7,9,16,20,……,相邻两项之和依次是4、9、16、25、36,是连续自然数的平方。图示如下:
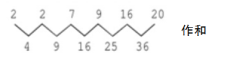
基本变化2:数列在连续变化过程中,以相邻项之和为基础。
【示例】1,3,8,33,164,985,……,数列从第三项开始,每一项都是它前面两项的和简单变化而来,(1+3)*2=8、(3+8)*3=33 、(8 +33)*4=164、(33+164)*5=985。图示如下:

![]()
12、积数列
【提点】积数列指的是数列的第一项和第二项,与第三项存在着倍数关系。
【示例】1,3,3,9,27,243,( )
【解析】可知1*3=3,3*3=9,3*9=27,9*27=243,可知此数列是乘积数列,故( )处填的是27×243,根据尾数法,最后一位应该是1。
基本变化1:前后项不是严格的乘积关系,存在乘积+数列,或者乘积+项。
【示例】5,3,16,49,( )
【解析】观察相邻三项之间的关系,发现5*3+1=16,3*16+1=49,第三项=第一项*第二项+1,故( )处填的是16×49+1=785。
![]()
13、倍数数列
【提点】后一项除以前一项的商有规律,也称为等比数列变式。当遇到相邻两项之间变化幅度在2-6倍的数列,都可以考虑倍数数列的思路。
【示例】1,2,6,24,120,······
基本变化1:倍数加数数列
【示例】1,3,10,32,99,()
【解析】此数列的特征,相邻两项之间的倍数在三倍左右,因此可以考虑是倍数关系。能够看出数字之间的倍数是基本能力,建议考生可以从较大的数字部分寻找倍数关系,一般倍数比较单一。所以发现,32和99之间最接近就是3倍,但是不是整数倍,还要找出加减数字的规律,32*3+3=99,10*3+2=32,3*3+1=10,1*3+0=3,所以答案是:99*3+4=301。
基本变化2:倍数加项数列
【示例】1,2,7,30,157,()
【解析】此数列的特征,相邻两项之间也是2-5倍左右,符合倍数数列的特征。仍然从较大的数字开始寻找倍数关系,30*5+7=157,7*4+2=30,2*3+1=7,3、4、5倍关系已经可以确定了,但是加的数字:1、2、7本身没有规律,所以应该结合原来数列的每一项分析,我们发现,加的数字正好是原来数列中的前一项,即:第二项的倍数+第一项=第三项,所以答案是:157*6+30=972。
![]()
14、分数数列
【提点】如果数列中出现了较多的分数,就可以基本认定这是一个分数数列。
(1)分子分母分别看规律。这种类型包含了两种情况。
情况一:直接分子分母分别去看
![]()
【解析】分子分母依此可以写为
![]()
所以分母分别为2、4、8、(16)、32、64、128的倍数为2的倍数数列。分子Wie平方数列1、4、9、(16)、25、36、49。所以括号为16/16=1。
![]()
情况二:出现假分数时,先把假分数换位真分数,再将分子分母分别去看
![]()
【解析】B。先把假分数换位真分数,分析分母依此可以写为
![]()
分子分母都是质数列。
(2)分子分母间存在某种计算关系。当发现分子分母间没有明确的规律时,可以考虑分子与分母的关系。
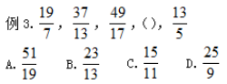
【解析】D。分子=分母*3-2。
(3)分数间项与项的关系
![]()
【解析】相邻两项的乘积作为一个常数列,依此为2倍、2.5倍、3倍、3.5倍,所以括号应为倒数第三项的4倍。因此4÷(35/16)=64/35。
(4)分数数列和多次方数列的区分
![]()
【解析】如果此题按分数的思路去做,发现就是没有答案,但是我们发现数列中的每一个数据都是多次方数列,依次为
![]()
![]()
15、组合数列
【提点】组合数列的形式是数列项数较多(大于6个)),难度适中。
(1)奇偶项交替变化递推型
隔项组合数列的特点是:两个数列(基本数列的任何一种或两种)进行隔项组合,奇数项和偶数项各为有规律可循的数列,此类题型难度最低,考查概率也最大。
【示例】1,1,1,2,2,4,6,7,()
【解析】个数较多,间隔组合数列,奇数项为1,1,2,6,作商后分别为1、2、3倍,故应为6的4倍为24。偶数项为1,2,4,7,11二级等差数列。
(2)两两分组递推型
【示例】11,22,20,40,12,24,34,()
【解析】个数较多,奇偶相间没有规律,考虑两两一组,则每组第二个数为第一个数的2倍。故答案为68。
(3)三三分组递推型
当考虑奇偶相间及两两一组没有规律,可以考虑为三三分组型。
【示例】4,5,15,6,7,35,8,9,()
【解析】个数较多,可能有部分考生看到4.、5,6、7,8、9,却割裂与15、35的关系,三三分组递推型4×5-5=15,6×7-7=35,8×9-9=63,故选答案为63。
- 2025-05-07
- 2025-04-25
- 2025-04-24
- 2025-04-19
- 2025-04-30
- 2025-05-07
- 2022-07-23
- 2021-03-19
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-05-07
- 2025-04-30
- 2025-04-30
- 2025-04-30
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2024-06-03
- 2021-02-24
- 2021-02-24
- 2021-02-24
- 2021-02-24
- 2021-02-24
- 2021-02-24













